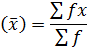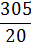

Mean of Continuous Data
We already know how to find the Mean of a Frequency Table (refer to Mean of a Frequency Table)
When continuous data is grouped, estimate the mean by using the midpoint of the grouped data. Add an extra column for the midpoint (x) and calculate the frequency fx using this midpoint.
- Example 1. Following is the marks scored in a class. Find the mean:
| Marks | Frequency f |
| 5 < M ≤ 10 | 2 |
| 10 < M ≤ 15 | 8 |
| 15 < M ≤ 20 | 7 |
| 20 < M ≤ 25 | 3 |
(a) For each range of Marks work out the midpoint x
| | | | | Marks | f | Midpoint x | | 5<M≤10 | 2 | 7.5 | | 10<M≤15 | 8 | 12.5 | | 15<M≤20 | 7 | 17.5 | | 20<M≤25 | 3 | 22.5 |
|
(b) Work out fx for each value of midpoint x. Multiply f by x
| | | | | Marks | f | x | fx | | 5<M≤10 | 2 | 7.5 | 2 × 7.5 = 15.0 | | 10<M≤15 | 8 | 12.5 | 8 × 12.5 = 100.0 | | 15<M≤20 | 7 | 17.5 | 7 × 17.5 = 122.5 | | 20<M≤25 | 3 | 22.5 | 3 × 22.5 = 67.5 |
|
(c) Work out the sum Σ of columns f and then fx
| | | | | Marks | f | x | fx | | 5<M≤10 | 2 | 7.5 | 2 × 7.5 = 15.0 | | 10<M≤15 | 8 | 12.5 | 8 × 12.5 = 100.0 | | 15<M≤20 | 7 | 17.5 | 7 × 17.5 = 122.5 | | 20<M≤25 | 3 | 22.5 | 3 × 22.5 = 67.5 | | Σ f | 20 | | Σ fx = 305.0 |
|
(d) Work out the Mean
| | Mean | 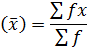 | = | 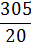 | = 15.25 |

to: