Answers − Simultaneous Equations by Substitution

1.   Solve these equations by substitution

   6x + y = 30
   5x − y = 14

  i. Label each equation

	Equation				Label
	6x + y	=	30		(1)
	5x − y	=	14		(2)

  ii. Rearrange equation (1) to make y the subject

		6x + y	=	30			note (3)
	−	6x	=		− 6x

y = 30 − 6x

   Note: (3) inverse of + 6x is − 6x

  iii. Substitute y = 30 − 6x into equation (2):

	5x	−	y	=	14
	5x	−	(30 − 6x)	=	14		note (4)
	5x	−	30  +  6x	=	14

   Note: (4) − ( − 6) = + 6

  iv. Rearrange to find the value of x

	5x	−	30 + 6x	=	14		note (5)
		+	30	=	+ 30

			11x	=		44		note (6)
		÷	11	=	÷	11

x

=

4

   Note: (5) inverse of − 30 is + 30
   Note: (6) inverse of × 11 is ÷ 11

  v. put x = 4 int0:

So x = 4 and y = 6

2.   Solve these equations by substitution

   5a + 2b = 54
   4a + b = 36

  answer: a = 6 and b = 12

3.   Solve these equations by substitution

   8x + 3y = 47
   3x − y = 24

  i. Label each equation

	Equation				Label
	8x + 3y	=	24		(1)
	3x − y	=	24		(2)

  ii. Rearrange equation (2) to make y the subject

3x

−

y

=

24

note (3)

+

y

=

+ y

		3x			=		24	+	y		note (4)
			−	24	=	−	24

3x

−

24

=

+

y

   Note: (3) inverse of − y is + y
   Note: (4) inverse of + 24 is − 24

So

y = 3x − 24

  iii. Substitute y = 3x − 24 into equation (1):

	8x	+	3(y)	=	47
	8x	+	3(3x − 24)	=	47
	8x	+	9x  −  72	=	47

  iv. Rearrange to find the value of x

	8x	+	9x	−	72	=			47		note (5)
				+	72	=		+	72

			17x		=		119		note (6)
		÷	17		=	÷	17

x

=

7

   Note: (5) inverse of − 72 is + 72
   Note: (6) inverse of × 17 is ÷ 17

  v. put x = 7 into:

So x = 7 and y = −3

4.   Solve these equations by substitution

   9x + y = 50
   7x − y = 78

  answer: x = 8 and y = −22

5.   Solve these equations by substitution

   5a + 3b = 18
   4a − 5b = 44

  i. Label each equation

	Equation				Label
	5a + 3b	=	18		(1)
	4a − 5b	=	44		(2)

  ii. Rearrange equation (1) to make b the subject

		5a	+	3b	=	18				note (3)
	−	5a			=		−	5a

			3b	=	(18	−	5a)		note (4)
		÷	3	=		÷	3

So

b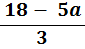

=

   Note: (3) inverse of + 5a is − 5a
   Note: (4) inverse of × 3 is ÷ 3

iii. Put b =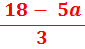

into (2):

	4a	−5	(	b	)	=	44
	4a	−5	(		)	=	44		note(5)

	12a	−	5(18 − 5a)	=	132		note(6)
	12a	−	90 + 25a	=	132		note(7)

   Note: (5) inverse of × 3 is ÷ 3
   Note: (6) multiply both sides by 3
   Note: (7) expand the brackets by multiplying

  iv. Rearrange to find the value of a

	12a	−	90	+	25a	=	132		note (8)
		+	90			=	+90

			37a	=	222		note (9)
		÷	37	=	÷37

a

=

6

Note: (8) inverse of − 90 is + 90
Note: (9) inverse of × 37 is ÷ 37

  v. Put a = 6 into:

So a = 6 and b = −4

6.   Solve these equations by substitution

   7x + y = 67
   5x + y = 45

  answer: x = 11 and y = −10

7.   Solve these equations by substitution

   11x + y = 90
   8x + 7y = 78

  i. Label each equation

	Equation				Label
	11x + y	=	90		(1)
	8x + 7y	=	78		(2)

  ii. Rearrange equation (1) to make y the subject

		11x	+	y	=	90			note (3)
	−	11x			=		− 11x

y

=

90

−11x

   Note: (3) inverse of + 11x is − 11x

  iii. Substitute y = 90 − 11x into equation (2):

	8x	+	7(y)	=	78
	8x	+	7(90 − 11x)	=	78
	8x	+	630  −  77x	=	78

  iv. Rearrange to find the value of x

	8x	+	630	−	77x	=	78		note (4)
		−	630			=	−630

		−69x	=	−552		note (5)
		÷69	=	÷69

x

=

8

   Note: (4) inverse of + 630 − 630
   Note: (5) inverse of × 69 is ÷ 69

  v. Put x = 8 into:

So x = 8 and y = 2

8.   Solve these equations by substitution

   12x + 4y = 84
   7x + 2y = 56

  answer: x = 14 and y = −21

         back to: