Solving Equations − 2
Here we use a combination of Solving Equations − Add and Subtract and Solving Equations − Multiply and Divide. Please look at the above before continuing
Example 1. 3(6 + b) = 15 What is the value of b?
Example 2.
Example 3. 40 + 2d = 5d − 20 What is the value of d?
| i. | Expand by multiplying out the brackets on the left hand side (LHS) of the equation |
| 3(6 + b) | = | 15 | ||||
| 18 | + | 3b | = | 15 | ||
| ii. | Subtract 18 from both sides |
| 18 | + | 3b | = | 15 | ||
| − | 18 | = | − | 18 |
| 3b | = | − 3 |
| iii. | Divide both sides by 3 |
| 3b | = | − 3 | ||
| ÷ | 3 | = | ÷ 3 |
| b | = | − 1 |
| iv. | To verify, put the value of b = − 1 back into the original equation: |
3(6 + (−1)) = 3(6 − 1) = 3(5) = 15
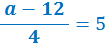 | What is the value of a? |
| i. | The inverse of divide by 4 is multiply by 4. So multiply both sides by 4 |
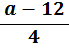 | = | 5 | |
| × 4 | = | × 4 |
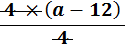 | = | 20 |
| a − 12 | = | 20 |
| ii. | The inverse of − 12 is + 12. So add 12 to both sides |
| a − 12 | = | 20 | |
| + 12 | = | +12 |
| a | = | 32 |
| iii. | To check, put the value of a = 32 back into the original equation: |
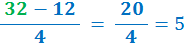
| i. | The inverse of − 20 is + 20. So add 20 to both sides |
| 40 | + | 2d | = | 5d | − | 20 | ||
| + | 20 | = | + | 20 |
| 60 | + | 2d | = | 5d |
| ii. | Move variable d to one side so inverse of + 2d is − 2d. So subtract 2d from both sides |
| 60 | + | 2d | = | 5d | |
| − | 2d | = | − 2d |
| 60 | = | 3d |
| iii. | Divide both sides by 3 |
| 60 | = | 3d | ||||
| ÷ | 3 | = | ÷ | 3 |
| 20 | = | d |
| iv. | To verify, put the value of d = 20 back into the original equation: |
both sides are equal
Note: 'what is the value of y' is the same as 'solve y'
to: 
